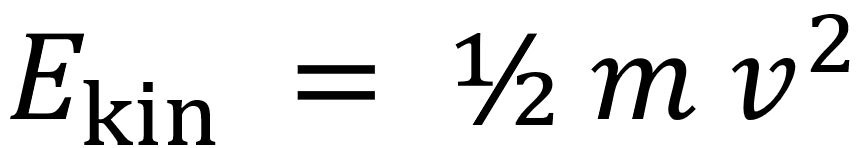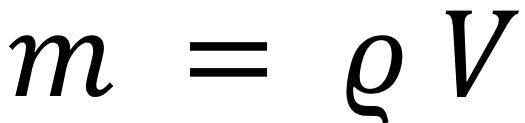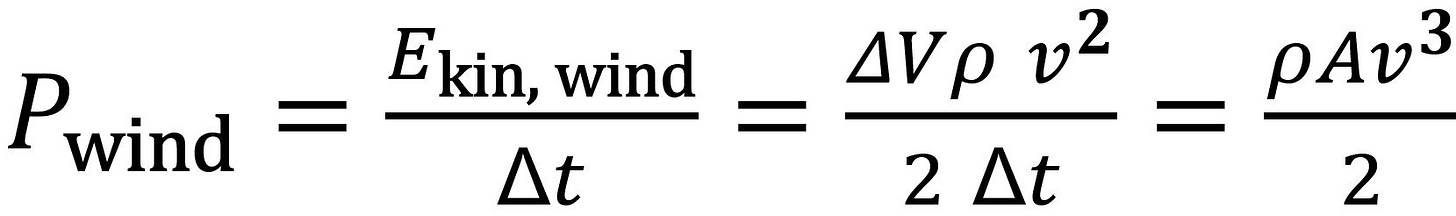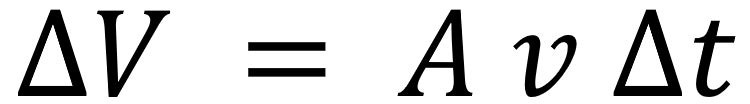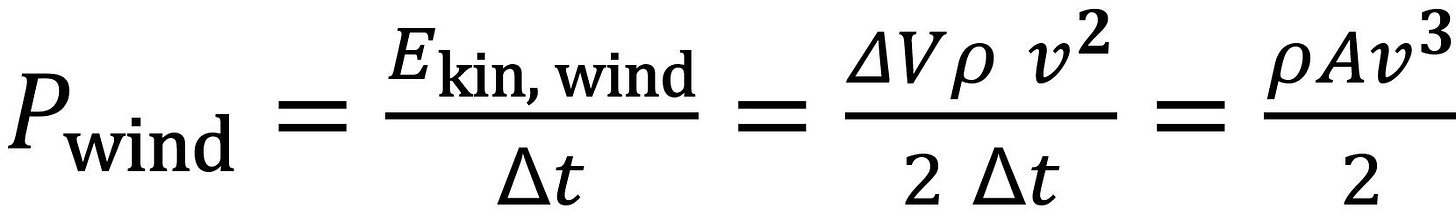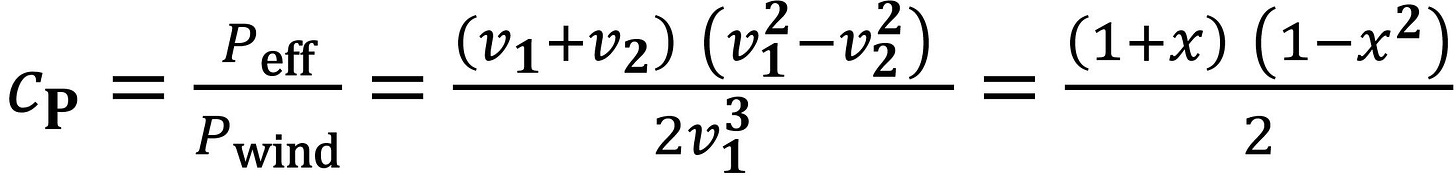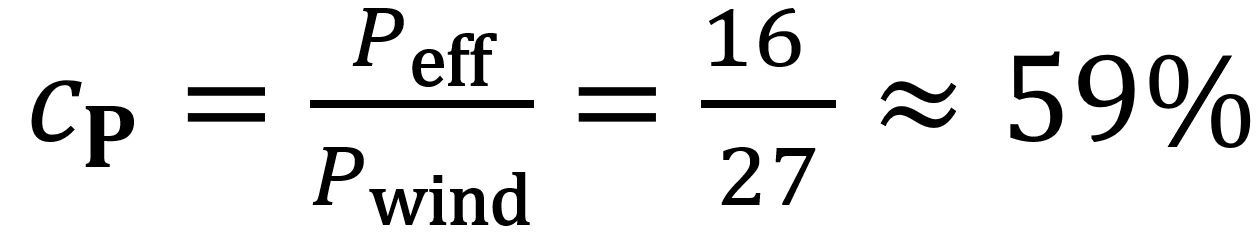One hundred miles off the coast of Yorkshire, UK, a boat laden with elegant white wings pulls up to a spot in the middle of the water. Orange buoys bob in the calm grey waters, marking out a grid of triangles and squares. The wind whips around the bulky ship, an invisible nod to the vast and soon-to-be-tapped potential.
Dogger Bank is the world's largest wind project. Once completed, it is expected to power six million homes, delivering eighteen terawatt-hours of power annually. Its two hundred and seventy-seven enormous wind turbines, each twice as high as the London Eye, stretch across an area of thousands of square kilometres. One single turbine is projected to cover the power needs of more than fifty-one thousand people.
A project of this scale is rare, but reflects an increasing trend amongst wind developers toward bigger farms and larger turbines. General Electric's Haliade-X boasts proudly of the increased efficiency that its sky-scraping two hundred and sixty-metre height delivers. Whereas smaller wind turbines perform at around twenty or thirty percent of their maximum theoretical capacity, Haliade-X reaches sixty percent.
Despite being at the cutting edge, the new model has already been leapfrogged, its fourteen-megawatt capacity bested by a new eighteen-megawatt model about to be deployed in China. The Haizhuang H260, deployed by the China State Shipbuilding Corporation, is the state-run enterprise's contribution to the Chinese Communist Party's 30.60 target to achieve peak CO2 output by 2030 and achieve net neutrality by 2060. Just six years ago, the maximum output for an offshore wind turbine was less than half what it is today.
Deep Dive: Why Are Wind Turbines Getting Bigger?
Wind turbines benefit from Moore's law-esque dividends from increases in size thanks to exponential and linear benefits to the area swept by their rotors and faster wind speed at altitude, and proportionate decreases in labour and maintenance cost. Let's briefly explain why from a technical perspective:
Firstly, the area swept by the blades increases exponentially with size
When the blades of a wind turbine rotate, they can be thought of as forming a circle. The circle created by the rotation of the tip of the blades in the air is defined as the swept area. The energy a wind turbine generates is proportionate to the size of this swept area. The larger the swept area, the more wind energy the rest of the turbine system can tap into. Swept area is the first contributor to the Moore's law-esque dividends of turbine size because it increases faster than blade length.
If we take blade length as the radius, we can compute the swept area using πr^2 (the area of a circle). When we increase the blade length, we can think of the increase in swept area as adding an additional ring to the original swept area. If we flatten this ring out, it is something like a rectangle.
The area of a rectangle is length x height. In this case, the length would be the circumference of the original swept area, and the height the increase in blade length. So we can multiply these two together to find the increase. The circumference of a circle is πd, or 2πr. Therefore the final equation for the approximation is:
Flattening out the ring to a rectangle is not entirely accurate, but the approximation is applicable because the error of this approximation decreases as we consider larger blade lengths and smaller size increases: we get good accuracy so long as we are describing incremental changes, the very purpose of this exercise.
Thus in summary, for every 1 unit the blade length increases by, swept area increases by 2π times the original blade length.
So for example, if the original blade length was 10 metres, increasing it by just 1 metre would add about 60 metres squared to the swept area. If the original blade length was 20 metres, the increase in swept area would be a staggering ~125 metres squared.
Secondly, wind speeds are much higher at skyscraping heights
When wind turbines increase in size, it's not just their blades that get larger. To accomodate the wider sweeping circle, they are also built taller. This means that the top of the highest blade will reach further into the atmosphere.
Wind speeds are greater at higher altitudes because wind further above the ground is less impeded by the terrain. A wind gust travelling at 4 metres will have to pass between foliage and buildings; a wind gust at 40 or 400 metres will have less of a problem.
Furthermore, the pressure differences which cause the flow of air (wind) are greater at higher altitudes. Whereas air pressure differences close to the ground are moderated by the thermal properties of the earth, further away from the earththe differences are more extreme. This creates stronger gusts of wind.
Wind speeds are consistently greater at higher altitudes, regardless of location. The table in the appendix shows how across nine vastly different locations in Malaysia, a large and meteorologically heterogeneous country, average wind speeds are virtually always higher at 100 metres compared to 10 metres.
Although differences in wind speed at altitude are themselves substantial, their impact on energy generation is exponential because a doubling of wind speed increases wind power by eight (see appendix for the proof)
Thus, a taller wind turbine consistently benefits from faster wind speeds.
Thirdly, small turbines struggle to balance wind permeability with energy capture
Betz's law describes the theoretical limits of how much wind power a perfect turbine could actually capture, and implies that larger turbines with more spaced out blades can harness more energy from the wind.
It tells us in just a few logical steps that a perfect wind capture device, free from constraints like engineering, cost, and more complex fluid dynamics like heat transfer, turbulence and compression, would capture exactly 59.3% of the wind's power.
In layman terms, Betz's law functions on the principle that wind capture devices must take some speed out of the wind by capturing its power. Thus, the amount of power captured must relate to the difference in the wind speed before and after the turbine. If the difference is zero, no power is captured. But if the wind speed after the turbine is close to zero, the turbine is acting like a wall, and not letting any air through. A wall-like turbine would result in the greatest difference in speed for any given wind speed, but the air would be blowing around it rather than through it. So, in order to capture energy from the wind, a turbine must allow some air through, and act more like a filter than a wall.
The fundamental constraint for the efficient design of a wind turbine is therefore determined by balancing permeability with energy capture. The equations which form the basis of Betz's law are laid out here. However, the fact that turbine efficacy is based on partial permeability implies that faster-spinning turbines need to have more spaced out blades. A turbine that span very fast and had many blades would appear to be a wall to the wind. Since a faster-spinning turbine implies more wind energy has been captured, however, we want our wind turbines to spin fast. Thus, the logical solution is to build very large wind turbines, which only have a few blades, that can spin very fast.
Most wind turbines currently have three blades, with historical windmills using anywhere from 4 to 32. Some companies are experimenting with two-bladed turbines, which are lighter, cheaper, bidirectional, and offer various benefits like storm survivability thanks to being able to lock their blades horizontal. However, other engineering challenges mean that they may not necessarily be practical, even in the long term. Thus, so long as we stick to three-blade turbines, there is an upper speed limit that can only be circumvented by increasing scale.
Fourth, a hundred large turbines are cheaper than a thousand small ones
However, regardless of output gains on a physical level, it is the efficiency gains on an economic level which drive larger turbine construction at the end of the day. A turbine with twice the swept area may require substantially more materials, but in terms of moving parts, it will use exactly the same amount. One larger turbine is also much easier to control through software than many smaller turbines, especially given that turbines need to be rotated dynamically into the wind in order to maximise power capture from the moving air. Given the size of offshore wind farms today, achieving the power output of an array like Dogger Bank with smaller residential turbines that were used in earlier generations would require tens of thousands of turbines, rather than just a few hundred. Added to this much greater level of complexity in terms of individually servicable components and moving parts would be the huge mass of wiring and control systems required to connect them all up. Thus, maintenance, planning, and labour costs decrease with turbine scale.
The caveat is that the stiffness of existing turbines results in weight limiting size
The factor that pushes in the opposite direction of all these gains to scale, however, is the very same dimensionality relation. Scaling up the height of a turbine by 2x increases the amount of materials needed by 8, other engineering considerations being equal. A turbine twice as tall also needs to be twice as wide and twice as deep. Efforts can be made to ensure construction materials as light as possible - using a careful blend of fibreglass, epoxy, polyester, aluminium and steel - but the rapid increase in mass relative to turbine size still nixes some of the productivity gains.
This infamous square-cube law contributes to some difficult-to-surpass limits when it comes to maximising turbine size. Whereas earlier turbines may have been just a few dozen tonnes, Dogger Bank's GE Haliade-X weighs in at 825 tonnes - which is considered impressively light given its size. Even the central unit alone, the nacelle, is an imposing eleven-metre-wide chunk of white-painted plastic and steel. For comparison, that means that Dogger Bank's 277-wind turbine array will weigh as much as 140,000 cars.
Further development of wind turbines will require creative design, from flexible and multipart blades to new and innovative materials. Reports that the China State Shipbuilding Corporation (CSSC) is pushing to create turbines over 300 metres high will easily push the weight of a single turbine over a thousand tonnes, meaning that power generation capacity could exceed twenty-five megawatts, enough to supply energy to entire segments of the population. In a more frugal market, a single turbine could meet the household power requirements of one hundred thousand people. Just one array of turbines could nourish an entire city.
But the strength and load-bearing characteristics of the materials we have available become a major consideration once the mass of the turbine parts reaches these sky-high limits. Unlike a building, which only has to take the downward force of its bricks and mortar most of the time, whilst in operation, a turbine is almost always moving. The length of the blades, which now can exceed one hundred metres from base to tip, means that the rotational speed of the outer blade is extremely fast. During steady winds, the tip can easily reach one hundred and fifty kilometres per hour, in fast winds, over three hundred kilometres per hour. The outer blade can therefore travel at a quarter of the speed of sound. As such, small twists or flexes in the blade can generate huge lateral forces. Yet at 200 metres-plus scale, the turbine is so large that different winds can affect the bottom and top of the turbine. This can create torsion and "twist" the components of the turbine in ways that amplify the load and do nothing to generate power.
One solution to this problem, learned from typhoon-proof skyscraper design, is to simply increase the flexibility. A non-rigid turbine blade can absorb some of the force of crosswinds by flexing. The dilemma that results is creating a hub design that prevents the blades from hitting the central tower. Turbines installed in open seas could see winds of hundreds of kilometres per hour in stormy conditions; a blade designed to catch the wind could easily flex too far and cause damage.
The takeaway: material change or engineering flexibility are needed to push wind power to new heights
The capture of wind opportunities is limited both literally and figuratively by inflexible engineering. To push past the size of current turbines into the next category of scale will test either the limits of our most advanced materials, adding to cost, or require us to radically rethink turbine design. Turbines that flex in the wind like palm fronds, to capture unprecedented amounts of energy with minimal additional load in tandem, could reduce the total amount of turbines the world needs from 1.3 million to a much more reasonable number. Only time will tell if humanity is able to rise up to this grand engineering challenge.
Appendix
Clarifications & equations
Wind speeds at altitude across Malaysia
Wind speeds are consistently greater at higher altitudes, regardless of location. This table shows how across 9 vastly different locations in Malaysia, a large and meteorologically heterogeneous country, average wind speeds are virtually always higher at 100 metres compared to 10 metres:
Source: Wind Mapping in Malaysia using Inverse Distance-Weighted Method
Proof that wind power is proportional to wind speed cubed
We first show that for all wind turbines, wind power is proportional to wind speed cubed. Wind energy is the kinetic energy of the moving air. The kinetic energy of a mass m with the velocity v is:
The air mass m can be determined from the air density ρ and the air volume V according to:
Then,
Power is energy divided by time. We consider a small time, Δt, in which the air particles travel a distance s = v Δt to flow through. We multiply the distance with the rotor area of the wind turbine, A, resulting in a volume of:
which drives the wind turbine for the small period of time. Then the wind power is given as:
The wind power increases with the cube of the wind speed. In other words: doubling the wind speed gives eight times the wind power. Therefore, the selection of a "windy" location is very important for a wind turbine.
Explanation of Betz’s law
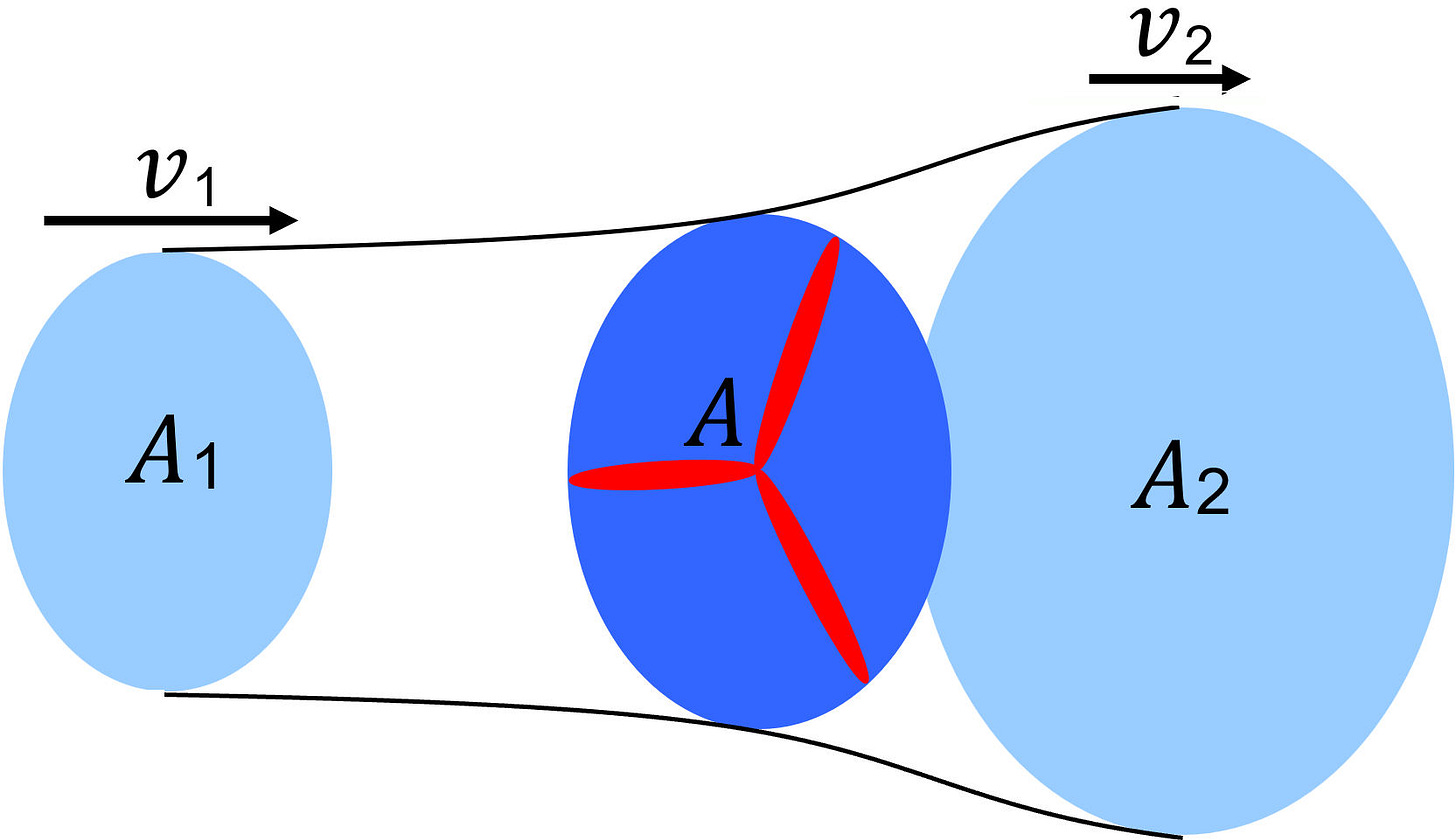
The effective usable wind power is less than indicated by the above equation. The wind speed behind the wind turbine can not be zero, since no air could follow. Therefore, only a part of the kinetic energy can be extracted. Consider the following picture:
The wind speed before the wind turbine is larger than after. Because the mass flow must be continuous, A v = constant, the area A2 after the wind turbine is bigger than the area A1 before. The effective power is the difference between the two wind powers:
If the difference of both speeds is zero, we have no net efficiency. If the difference is too big, the air flow through the rotor is hindered too much. The power coefficient cp characterizes the relative drawing power:
To derive the above equation, the following was assumed: A_1_v_1 = _A_2_v_2 = A (_v_1+_v_2) / 2. We designate the ratio _v_2/_v_1 on the right side of the equation with _x. To find the value of x that gives the maximum value of CP, we take the derivative with respect to x and set it to zero. This gives a maximum when x = 1/3. Maximum drawing power is then obtained for _v_2 = _v_1 / 3, and the ideal power coefficient is given by:
Resources on wind turbine spacing
There is also a related conversation on how far apart wind turbines should be spaced, which is salient because increasing rotor size implies vastly larger wind farms. Given a rotor circumference of 300m, and the minimum of five rotor diameters, next-generation turbines could not be less than 1.5km apart. For a turbine field of two hundred to three hundred units, that implies an area of hundreds of square kilometres. The covered area could number into the thousands of square kilometres if this source deriving from is correct, and ideal turbine spacing is fifteen rotor diameters. This figure is derived from Dr. Charles Meneveau, a researcher at Johns Hopkins University.
Sources & Links
Dogger Bank: https://www.theguardian.com/business/2021/jan/02/dogger-banks-giant-turbines-herald-a-wind-of-change-in-uk-industry
Wind speeds at altitude: https://www.researchgate.net/publication/259991146_Wind_Mapping_in_Malaysia_Using_Inverse_Distance_Weighted_Method
Maximum efficiency of a wind turbine: https://digitalcommons.usf.edu/cgi/viewcontent.cgi?article=4865&context=ujmm
Betz’s Law: https://home.uni-leipzig.de/energy/energy-fundamentals/15.htm
Number of blades on a wind turbine: https://windenergysolutions.nl/uncategorized/how-many-blades/
Record-breaking wind turbine from the Chinese State Shipbuilding Corporation: http://www.xinhuanet.com/english/special/2021-07/01/c_1310038592.htm
Flexible blade wind turbines: https://www.scientificamerican.com/article/world-rsquo-s-largest-wind-turbine-would-be-taller-than-the-empire-state-building/
Two-blade wind turbines: https://maritime-executive.com/article/two-blade-turbines-the-future-of-offshore-wind-energy
Calculating how many people a wind turbine can supply power to (number of people per household in the UK): https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/families/bulletins/familiesandhouseholds/2022
China’s 30.60 goal: https://rhg.com/research/china-30-60-tracking-the-financing-of-chinas-green-transition/
Cost per megawatt of wind energy: https://www.oedigital.com/news/481796-offshore-wind-turbines-size-really-matters-rystad-says